Link to the paper: IEEE

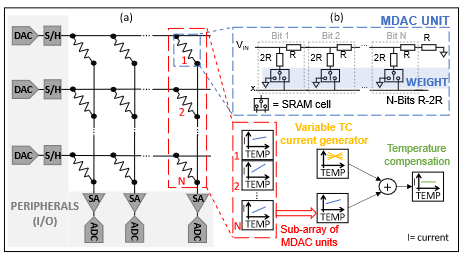
In a nutshell: A simple process and temperature compensation circuitry to be added to resistive-based analog In-Memory Computing (IMC) arrays. This avoids degrading the accuracy of the array (and by extension the AI task that it computes) because of process and temperature non-idealities.

Why? Analog and mixed-signal IMC circuits are becoming popular to build hardware-efficient accelerators for AI computation. Yet, the sensitivity of these circuits to process and temperature variations is typically overlooked. Still, it has been shown that these variations create inaccuracies and degrade the performance of the AI task, which is an issue...

How? We added a simple yet effective compensation circuitry, that can generate current with variable temperature coefficient to compensate for the variations at the bottom of a IMC column. The compensation circuitry has been taped out and measured, showing that non-idealites due to process and temperature variations can be well compensated. Now needs to be tested on bigger arrays!

Some personal context/comments: My team, along with Aalto's Electronic Circuit Design unit, has been working on IMC accelerators for a few years now (hopefully we get more extensive results to show soon). One thing that we realized is that in terms of mixed-signal accelerators, there is a critical need to evaluate the robustness/reliability of the analog circuitry itself (not only eventual emerging memory technologies we use to build the chip). So we started to look into this, in particular going back to simple compensation techniques and see how effective they can be. This is the first paper we get to publish on this topic!

Link to the paper: arXiv

In a nutshell: a methodology to decompose sparse tensors and reorder them as non-sparse representations ("cascade of Einsums") for more efficient hardware acceleration. The process is based on fibertree decomposition and further improves existing accelerators such as Gamma or OuterSPACE

Why? ML models, in particular deep NNs, move towards more sparse representations (due to e.g. pruned or quantized networks, the emergence of graphs models, etc.). With sparse models, most existing hardware accelerators have a harder time, i.e., HW accelerators prefer "full" matrices.

How? The work abstracts sparse tensors into fiber trees, which are then used to modify the order of computations (the tensor ranks) to build a tree of dependent Einsum operations (which are not sparse) to be accelerated on existing hardware platforms.

In more details. Lately, I have been interested in sparse Neural Networks (NN) hardware acceleration. NNs are becoming sparse for various reasons, e.g., pruning unuseful weights, quantizing the model's parameters, and removing (parts of) NN layers to compress the model. All aim to increase energy efficiency and embed these NNs on the edge.

NN computation can be represented by successive tensor operations involving the inputs, weights, and activations of each neuron and each layer (See e.g., HERE ). So AI acceleration can essentially mean acceleration of tensors.

Yet, typical AI accelerators are efficient when processing NN layers with a high degree of parallelism, i.e., full tensors where "everyone connects to everyone". Spartity introduces zeros and cuts this parallelism and, with it, the accelerator's efficiency.

How do we make sparse tensors non-sparse again without recreating all computations we tried to avoid in the first place? An elegant solution in this TeAAL paper is to decompose the successive (sparse) tensors induced by a given NN computation and reorder them into a tree of non-sparse operations in a different order than initially laid out. So, we get an intermediate representation of non-sparse operations, here Einsum operations, but arranged in a tree-fashion depending on their execution order. The decomposition uses fiber trees, which facilitate reordering the ranks of the tensors and execute them efficiently on hardware.

Einsums explained: HERE

OuterSPACE accelerator: HERE